
The UVSphere looks like a globe. For many purposes it is perfectly fine, but for some use cases, e.g. if you want to deform the sphere, it is disadvantageous that the density of vertices is greater around the poles. Here the icosphere is better, its vertices are distributed evenly.
Icospheres are a type of geodesic dome.
So I want to create a icosphere programmatically. Its base is an icosahedron (I guess this is where the ico in the name comes from), a regular polyhedron with 20 equilateral triangles.
An icosphere is then created by splitting each triangle into 4 smaller triangles. This can be done several times, the recursion level is a parameter to the icosphere.
Creating an Icosahedron
Wikipedia has a nice image that shows that the vertices of an icosahedron are the corners of three orthogonal rectangles:
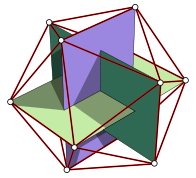
(source: Wikipedia)
With this the vertex creation is pretty straight-forward:
// create 12 vertices of a icosahedron
var t = (1.0 + Math.Sqrt(5.0)) / 2.0;
addVertex(new Point3D(-1, t, 0));
addVertex(new Point3D( 1, t, 0));
addVertex(new Point3D(-1, -t, 0));
addVertex(new Point3D( 1, -t, 0));
addVertex(new Point3D( 0, -1, t));
addVertex(new Point3D( 0, 1, t));
addVertex(new Point3D( 0, -1, -t));
addVertex(new Point3D( 0, 1, -t));
addVertex(new Point3D( t, 0, -1));
addVertex(new Point3D( t, 0, 1));
addVertex(new Point3D(-t, 0, -1));
addVertex(new Point3D(-t, 0, 1));
To build the triangles, I have numbered the vertices in the order I used in the piece of code above:
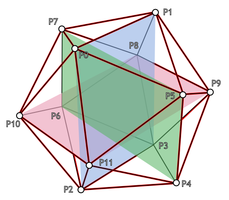
All triangles must have their vertices in the same order, I used counter-clockwise direction. Now it is just a matter of carefully looking at the diagram:
// create 20 triangles of the icosahedron
var faces = new List<TriangleIndices>();
// 5 faces around point 0
faces.Add(new TriangleIndices(0, 11, 5));
faces.Add(new TriangleIndices(0, 5, 1));
faces.Add(new TriangleIndices(0, 1, 7));
faces.Add(new TriangleIndices(0, 7, 10));
faces.Add(new TriangleIndices(0, 10, 11));
// 5 adjacent faces
faces.Add(new TriangleIndices(1, 5, 9));
faces.Add(new TriangleIndices(5, 11, 4));
faces.Add(new TriangleIndices(11, 10, 2));
faces.Add(new TriangleIndices(10, 7, 6));
faces.Add(new TriangleIndices(7, 1, 8));
// 5 faces around point 3
faces.Add(new TriangleIndices(3, 9, 4));
faces.Add(new TriangleIndices(3, 4, 2));
faces.Add(new TriangleIndices(3, 2, 6));
faces.Add(new TriangleIndices(3, 6, 8));
faces.Add(new TriangleIndices(3, 8, 9));
// 5 adjacent faces
faces.Add(new TriangleIndices(4, 9, 5));
faces.Add(new TriangleIndices(2, 4, 11));
faces.Add(new TriangleIndices(6, 2, 10));
faces.Add(new TriangleIndices(8, 6, 7));
faces.Add(new TriangleIndices(9, 8, 1));
Refining to an Icosphere
Now we need to refine the triangles to create an icosphere from it. Each edge of the triangle is split in half, one triangle is formed by the three points sitting in the middle of these edges and three triangles surrounding it:
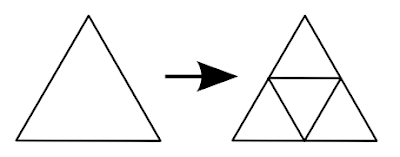
// refine triangles
for (int i = 0; i < recursionLevel; i++)
{
var faces2 = new List<TriangleIndices>();
foreach (var tri in faces)
{
// replace triangle by 4 triangles
int a = getMiddlePoint(tri.v1, tri.v2);
int b = getMiddlePoint(tri.v2, tri.v3);
int c = getMiddlePoint(tri.v3, tri.v1);
faces2.Add(new TriangleIndices(tri.v1, a, c));
faces2.Add(new TriangleIndices(tri.v2, b, a));
faces2.Add(new TriangleIndices(tri.v3, c, b));
faces2.Add(new TriangleIndices(a, b, c));
}
faces = faces2;
}
The method getMiddlePoint() does a bit more than just splitting the edge in half. Firstly, it fixes it length so the new point will lie on the unit sphere (i.e. a sphere that sits in the origin and has a radius of 1). Otherwise we will end up with a refined icosahedron but not with an icosphere. By the way: this is done with the original vertices of the icosahedron too, as the one we created is bigger than the unit sphere.
Secondly, it caches the points and reuses them. As each edge belongs to two triangles, without the cache there will be two new middle points created for each edge. I implemented the cache using a dictionary. As the key I put the two vertex indices into an Int64. As the middle point of the edge from p1 to p2 is the same as for the edge from p2 to p1, for the key always the smaller index is stored as the first.
The following images shows created icospheres where the refinement step has been run once, twice and three times, respectively.

The complete C# code looks like following. It creates a MeshGeometry3D data structure to be used with XAML/WPF, but as most mesh structures work very similar it should be easy to rewrite it for other frameworks.
public class IcoSphereCreator
{
private struct TriangleIndices
{
public int v1;
public int v2;
public int v3;
public TriangleIndices(int v1, int v2, int v3)
{
this.v1 = v1;
this.v2 = v2;
this.v3 = v3;
}
}
private MeshGeometry3D geometry;
private int index;
private Dictionary<Int64, int> middlePointIndexCache;
// add vertex to mesh, fix position to be on unit sphere, return index
private int addVertex(Point3D p)
{
double length = Math.Sqrt(p.X * p.X + p.Y * p.Y + p.Z * p.Z);
geometry.Positions.Add(new Point3D(p.X/length, p.Y/length, p.Z/length));
return index++;
}
// return index of point in the middle of p1 and p2
private int getMiddlePoint(int p1, int p2)
{
// first check if we have it already
bool firstIsSmaller = p1 < p2;
Int64 smallerIndex = firstIsSmaller ? p1 : p2;
Int64 greaterIndex = firstIsSmaller ? p2 : p1;
Int64 key = (smallerIndex << 32) + greaterIndex;
int ret;
if (this.middlePointIndexCache.TryGetValue(key, out ret))
{
return ret;
}
// not in cache, calculate it
Point3D point1 = this.geometry.Positions[p1];
Point3D point2 = this.geometry.Positions[p2];
Point3D middle = new Point3D(
(point1.X + point2.X) / 2.0,
(point1.Y + point2.Y) / 2.0,
(point1.Z + point2.Z) / 2.0);
// add vertex makes sure point is on unit sphere
int i = addVertex(middle);
// store it, return index
this.middlePointIndexCache.Add(key, i);
return i;
}
public MeshGeometry3D Create(int recursionLevel)
{
this.geometry = new MeshGeometry3D();
this.middlePointIndexCache = new Dictionary<long, int>();
this.index = 0;
// create 12 vertices of a icosahedron
var t = (1.0 + Math.Sqrt(5.0)) / 2.0;
addVertex(new Point3D(-1, t, 0));
addVertex(new Point3D( 1, t, 0));
addVertex(new Point3D(-1, -t, 0));
addVertex(new Point3D( 1, -t, 0));
addVertex(new Point3D( 0, -1, t));
addVertex(new Point3D( 0, 1, t));
addVertex(new Point3D( 0, -1, -t));
addVertex(new Point3D( 0, 1, -t));
addVertex(new Point3D( t, 0, -1));
addVertex(new Point3D( t, 0, 1));
addVertex(new Point3D(-t, 0, -1));
addVertex(new Point3D(-t, 0, 1));
// create 20 triangles of the icosahedron
var faces = new List<TriangleIndices>();
// 5 faces around point 0
faces.Add(new TriangleIndices(0, 11, 5));
faces.Add(new TriangleIndices(0, 5, 1));
faces.Add(new TriangleIndices(0, 1, 7));
faces.Add(new TriangleIndices(0, 7, 10));
faces.Add(new TriangleIndices(0, 10, 11));
// 5 adjacent faces
faces.Add(new TriangleIndices(1, 5, 9));
faces.Add(new TriangleIndices(5, 11, 4));
faces.Add(new TriangleIndices(11, 10, 2));
faces.Add(new TriangleIndices(10, 7, 6));
faces.Add(new TriangleIndices(7, 1, 8));
// 5 faces around point 3
faces.Add(new TriangleIndices(3, 9, 4));
faces.Add(new TriangleIndices(3, 4, 2));
faces.Add(new TriangleIndices(3, 2, 6));
faces.Add(new TriangleIndices(3, 6, 8));
faces.Add(new TriangleIndices(3, 8, 9));
// 5 adjacent faces
faces.Add(new TriangleIndices(4, 9, 5));
faces.Add(new TriangleIndices(2, 4, 11));
faces.Add(new TriangleIndices(6, 2, 10));
faces.Add(new TriangleIndices(8, 6, 7));
faces.Add(new TriangleIndices(9, 8, 1));
// refine triangles
for (int i = 0; i < recursionLevel; i++)
{
var faces2 = new List<TriangleIndices>();
foreach (var tri in faces)
{
// replace triangle by 4 triangles
int a = getMiddlePoint(tri.v1, tri.v2);
int b = getMiddlePoint(tri.v2, tri.v3);
int c = getMiddlePoint(tri.v3, tri.v1);
faces2.Add(new TriangleIndices(tri.v1, a, c));
faces2.Add(new TriangleIndices(tri.v2, b, a));
faces2.Add(new TriangleIndices(tri.v3, c, b));
faces2.Add(new TriangleIndices(a, b, c));
}
faces = faces2;
}
// done, now add triangles to mesh
foreach (var tri in faces)
{
this.geometry.TriangleIndices.Add(tri.v1);
this.geometry.TriangleIndices.Add(tri.v2);
this.geometry.TriangleIndices.Add(tri.v3);
}
return this.geometry;
}
}

